Örgütler, büyük dil modellerini (LLM) özelleştirirken karşılaştıkları en büyük zorluklardan biri, çok sayıda deneme yapmaları ve bu denemelerin yalnızca bir tanesinin başarılı bir modelle sonuçlanmasıdır. Deneylerin maliyeti genellikle düşük olsa da, elde edilen sonuçların çaba değer olduğu kabul edilmektedir. Ancak, bu deney süreci bazı “israf” kaynakları gerektirmektedir; bu kaynaklar arasında kullanılmayan hesaplama gücü, harcanan geliştirici zamanı gibi unsurlar da bulunmaktadır.
Model birleştirme, birden fazla özelleştirilmiş LLM’nin ağırlıklarını birleştirerek kaynak kullanımını artırır ve başarılı modellerin değerini katlayarak artırır. Bu yaklaşım, iki ana çözüm sunmaktadır:
- Deneyim israfını azaltarak “başarısız deneyleri” yeniden kullanma imkanı sağlar.
- Eğitim sürecine katılmayı gerektirmeden maliyet açısından etkili bir alternatif sunar.
Bu yazı, modellerin nasıl özelleştirildiğini, model birleştirmenin nasıl çalıştığını, farklı model birleştirme türlerini ve model birleştirmenin nasıl evrimleştiğini incelemektedir.
Model Özelleştirmeyi Yeniden İncelemek
Bu bölüm, modellerin nasıl özelleştirildiğine dair kısa bir genel bakış sağlayacak ve bu sürecin model birleştirme konusunu daha iyi anlamak için nasıl değerlendirilebileceğini ele alacaktır.
Burada tartışılan bazı kavramlar, model birleştirme konusunu daha iyi anlamak amacıyla basitleştirilmiştir. Özelleştirme teknikleri, dönüştürücü mimari ve eğitim konularında ayrı olarak bilgi sahibi olmanız önerilmektedir. Örneğin, “LLM Tekniklerini Ustalıkla Kullanma: Özelleştirme” başlıklı kaynağa başvurabilirsiniz.
Ağırlık Matrislerinin Modellerdeki Rolü
Ağırlık matrisleri, birçok popüler model mimarisinin temel bileşenleridir ve modelin tahmin yapabilmesi için gerekli bilgileri depolayan geniş sayı gruplarıdır.
Veri bir modelin içinden geçerken, her biri kendi ağırlık matrisine sahip olan çok sayıda katmandan geçmektedir. Bu matrisler, girdi verilerini matematiksel işlemlerle dönüştürerek modelin verilerden öğrenmesini ve onlara uyum sağlamasını sağlar.
Bir modelin davranışını değiştirmek için bu matrisler içindeki ağırlıkların güncellenmesi gerekir. Ağırlıkların nasıl değiştirildiği konusunda detaylar ikinci planda kalırken, bir temel modelin özelleştirilmesi sırasında her seferinde benzersiz bir güncellenmiş ağırlık setinin elde edildiği önemlidir.
Görev Özelleştirmesi
Bir LLM’yi özetleme veya matematik gibi belirli bir görev için ince ayar yaptığınızda, ağırlık matrisleri üzerinde yapılan güncellemeler, özellikle o görevin performansını artırmaya yönelik olarak hedeflenmiştir. Bu, ağırlık matrislerindeki değişikliklerin homojen bir şekilde dağılmadığı anlamına gelmektedir.
Bu kavramı somut bir şekilde anlatmak için, ağırlık matrislerini 100 yard uzunluğunda bir spor sahası olarak düşünelim. Modeli özetleme amacıyla özelleştirirken, ağırlık matrislerine yapılan güncellemeler belirli alanlarda yoğunlaşabilir; örneğin, 10-30 yard aralığında. Matematik için özelleştirirken ise, güncellemeler 70-80 yardlar gibi farklı bir bölgeye odaklanır.
İlginç bir şekilde, benzer bir görev için özelleştirildiğinde, örneğin Fransızca özetleme gibi, güncellemeler aynı ağırlık matrisi bölgelerine çakışabilir; bu da bazı güncellemelerin örtüşme ihtimalini gösterir. Bu örtüşme, farklı görev özelleştirmelerinin ağırlık matrislerinin aynı bölgelerini önemli ölçüde etkileyebileceğine dair önemli bir içgörü sunar.
Önceki örnek amaçlı basitleştirilmiş olsa da, son derece doğrudur. Farklı görev özelleştirmeleri, ağırlık matrislerinin farklı bölümlerinde güncellemelerle sonuçlanır ve benzer görevler için özelleştirme, ilgili ağırlık matrislerinin ayni kısımlarını değiştirebilir.
Model Birleştirme
Model birleştirme, birden fazla modelin veya model güncellemelerinin bir bütün olarak bir araya getirilmesiyle ilgili stratejileri kapsayan geniş bir yöntem grubudur. Bu bölümde, bu tekniklerin Arcee AI tarafından geliştirilen mergekit isimli açık kaynaklı kütüphane aracılığıyla uygulanmasına odaklanılacaktır. Bu kütüphane, çeşitli birleştirme stratejilerinin uygulanmasını kolaylaştırmaktadır.
Birleştirmek için farklı karmaşık yöntemler kullanılmaktadır. Burada dört ana birleştirme yöntemine odaklanacağız:
- Model Çorbası
- Sferik Doğrusal İnterpolasyon (SLERP)
- Görev Aritmetiği (Görev Vektörleri Kullanarak)
- TIES (DARE ile birlikte)
Model Çorbası
Model Çorbası yöntemi, hiperparametre optimizasyon deneyleri ile oluşturulan model ağırlıklarının ortalamasını alarak çalışır. Model Çorbası: Birden Fazla İnce Ayar Yapılmış Modelin Ağırlıklarını Ortalama Alarak Performansı Artırmak başlıklı çalışmada bu durum detaylandırılmaktadır.
Başlangıçta bilgisayarla görme modelleri üzerinden test edilen bu yöntem, LLM’ler için de umut verici sonuçlar göstermiştir. Ek olarak, deneylerden bazı değerler elde ederken bu süreç basit ve hesaplama açısından yoğun değildir.
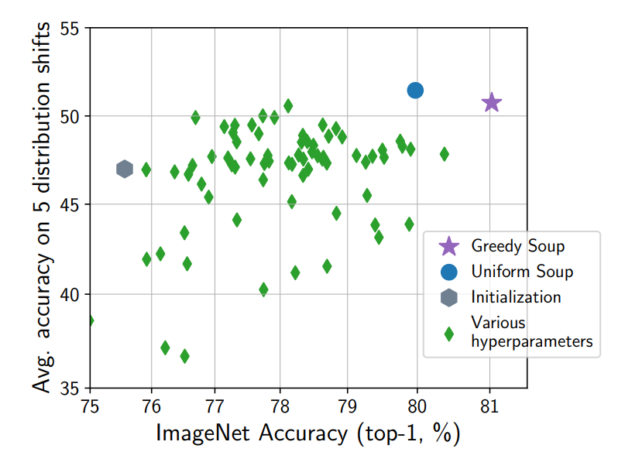
Model Çorbası oluşturmanın iki yolu vardır: saf ve açgözlü. Saf yaklaşım, tüm modellerin performansına bakılmaksızın sırasıyla birleştirilmesidir. Açıkgözlü uygulama ise şu basit algoritmayı izler:
- Modelleri istenilen görevdeki performanslarına göre sıralayın.
- En iyi performansa sahip modeli, ikinci en iyi performansa sahip model ile birleştirin.
- Birlestirilmiş modelin istenilen görevdeki performansını değerlendirin.
- Eğer birleşik model daha iyi performans gösteriyorsa, bir sonraki model ile devam edin; aksi halde mevcut modeli atlayarak sonraki en iyi model ile deneyin.
Bu açgözlü yaklaşım, elde edilen Model Çorbası’nın en iyi bireysel model kadar iyi olmasını garanti eder.
Model Çorbası oluşturma sürecinin her adımı, iki veya daha fazla model ağırlığını basit bir şekilde ağırlıklı ve normalleştirilmiş doğrusal ortalama alarak uygulanır. Hem ağırlıklandırma hem de normalizasyon isteğe bağlıdır, fakat tavsiye edilmektedir. Bu, mergekit kütüphanesinden uygulanması aşağıdaki gibidir:
res = (weights * tensors).sum(dim=0)
if self.normalize:
res = res / weights.sum(dim=0)
Bu yöntem, bilgisayarla görme ve dil alanında umut verici sonuçlar vermiş olsa da bazı ciddi sınırlamalara sahiptir. Özellikle, modelin daha performanslı olacağına dair bir garanti yoktur; doğrusal ortalama alma, performans kaybı veya genelleme kaybına yol açabilir.
Bir sonraki yöntem olan SLERP, bu spesifik sorunların bazılarının üstesinden gelmektedir.
SLERP
Sferik Doğrusal İnterpolasyon (SLERP), 1985 yılında yayımlanan Dönme Animasyonları İçin Quaternion Eğrileri başlıklı makalede tanıtılmış bir yöntemdir. İki vektör arasında ortalamayı daha akıllıca hesaplamaya yardımcı olur. Teknik açıdan, iki nokta arasındaki en kısa yolu, eğri bir yüzey üzerinde hesaplar.
Bu yöntem, iki modeli birleştirme konusunda mükemmel bir performans sergiler. Klasik örnek, dünyanın yüzeyinde iki nokta arasındaki en kısa yolun hesaplanmasıdır. Teknik olarak, en kısa yol dünyayı bir çizgi ile geçmek olacaktır; ancak gerçekte, bu yol dünyanın yüzeyinde eğri bir yol olacaktır. SLERP, modelleri bir araya getirirken bu akıcı yolu hesaplayarak, benzersiz model ağırlık “yüzeylerinin” korunmasını sağlar.
Aşağıdaki kod parçası, SLERP algoritmasının kalbidir ve iki model arasında iyi bir interpolasyon sağlanmasına olanak tanır:
# v0 ve v1 arasındaki başlangıç açısını hesaplayın
theta_0 = np.arccos(dot)
sin_theta_0 = np.sin(theta_0)
# Timestep t'deki açı
theta_t = theta_0 * t
sin_theta_t = np.sin(theta_t)
# SLERP algoritmasını tamamlayın
s0 = np.sin(theta_0 - theta_t) / sin_theta_0
s1 = sin_theta_t / sin_theta_0
res = s0 * v0_copy + s1 * v1_copy
return maybe_torch(res, is_torch)
Görev Aritmetiği (Görev Vektörleri Kullanarak)
Bu model birleştirme yöntemleri grubu, modelleri çeşitli şekillerde birleştirmek için Görev Vektörleri kullanarak karmaşıklık düzeyini artırır.
Görev Vektörleri: Özelleştirme Güncellemelerini Yakalamak
Modeller özelleştirildiğinde, güncellemeler modelin ağırlıklarına yapılmaktadır ve bu güncellemeler temel model matrislerinde tutulmaktadır. Nihai matrisleri, tamamen yeni bir model olarak değil, temel ağırlıklarla özelleştirilmiş ağırlıklar arasındaki fark (veya delta) olarak görebiliriz. Bu, görev vektörü kavramını tanıtır; bu yapı temel ağırlıklar ile özelleştirilmiş ağırlıklar arasındaki farkı içerir.
Bu, Düşük Sıralı Uyarlama (LoRA) temelinde yatan fikirdir, ancak ağırlık güncellemelerini temsil eden matrisleri faktörleştirme adımını içermemektedir.
Görev Müdahalesi: Çakışan Güncellemeler
Spor sahası örneğine dönecek olursak, farklı özelleştirmeler arasında güncellemelerin örtüşme ihtimali bulunmaktadır. Benzer görevler için yapılan özelleştirmenin, iki veya daha fazla Görev Vektörü arasında önemli çakışmalara neden olabileceğini anlamak yeterince sezgiseldir.
Bu “çakışan güncelleme” fikri, Görev Müdahalesi olarak daha biçimsel bir şekilde tanımlanır ve iki veya daha fazla Görev Vektörü arasında önemli güncellemelerin çakışma potansiyelini ilgilendirir.
Görev Aritmetiği
Görev Aritmetiği, Modelleri Görev Aritmetiği ile Düzenleme başlıklı çalışmada tanıtılan görev vektörü yaklaşımının en basit uygulamasıdır. Süreç şu şekilde işler:
- İki veya daha fazla görev vektörü elde edilir ve bunlar, Model Çorbasında olduğu gibi doğrusal olarak birleştirilir.
- Elde edilen birleşik görev vektörü temel modele eklenir.
Bu süreç basit ve etkilidir, ancak önemli bir zayıflık içerir: birleştirilmek istenen görev vektörleri arasındaki potansiyel müdahaleye dikkat edilmez.
TIES-Birleştirme
TIES-Birleştirme: Modelleri Birleştirirken Müdahaleyi Çözme başlıklı çalışmada tanıtılan TIES (TrIm Elect Sign and Merge), Görev Aritmetiği’nin temel fikirlerini alıp, Görev Vektörleri arasındaki olası müdahaleleri çözmek için sezgisel yaklaşımlar ile birleştirir.
Genel prosedür, birleştirilen her Görev Vektörü için ağırlığın büyüklüğünü, sonra gelen işaretlerini göz önünde bulundurmak ve ardından kalan ağırlıkları ortalamayı içerir.
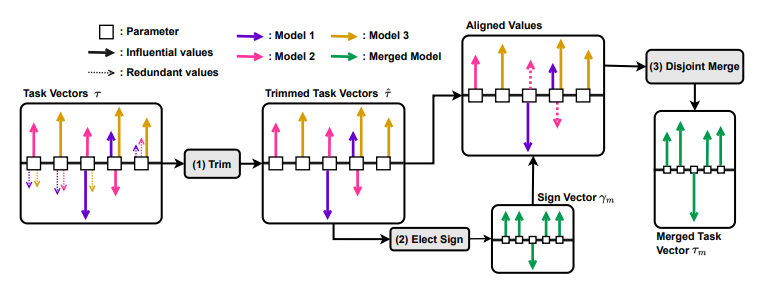
Bu yöntem, birleştirme sürecinde her bir ağırlık için en önemli güncellemeyi yapan modellere öncelik vererek müdahale sorununu çözmeye çalışır. Esasen, belirli bir ağırlığı daha fazla önemseyen modellere öncelik verilir.
DARE
Dil Modelleri Süper Mario Gibidir: Homolog Modellerden Yetenekleri Bedava Alma başlıklı çalışmada tanıtılan DARE, doğrudan bir model birleştirme tekniği olmaktan çok, diğer yaklaşımlar ile birlikte dikkate alınabilecek bir ekleme olarak ele alınabilir. DARE, şu temele dayanmaktadır:
Delta parametrelerini bir oran ile Açıp, REsystelik kalanları 1/(1 – p) ile yeniden ölçeklendirerek, orijinal gömme katmanlarına yakın bir tahmin yapar.
Müdahale sorununu sezgisel yöntemlerle ele almak yerine, DARE farklı bir perspektiften yaklaşmaktadır. Temelde, belirli bir görev vektöründeki güncellemelerin büyük bir kısmını rastgele sıfıra ayarlayarak ve kalan ağırlıkları atılan ağırlıkların oranına göre yeniden ölçeklendirerek gerçekleşir.
DARE, belirli görev vektörü ağırlıklarının %90’ını veya hatta %99’unu silerken bile etkili olduğu gösterilmiştir.
Model Birleştirme ile Model Kullanımını Artırma
Model birleştirme kavramı, birden fazla LLM’nin faydasını maksimize etmenin pratik bir yolunu sunmaktadır. Ayrıca, daha büyük bir topluluk tarafından yapılan görev-specific ince ayarları da içermektedir. Model Çorbası, SLERP, Görev Aritmetiği, TIES-Birleştirme ve DARE gibi teknikler aracılığıyla, organizasyonlar birbiriyle ilişkili modelleri etkili bir şekilde birleştirerek, deneyimleri ve organizasyonlar arası çabaları yeniden kullanabilir.
Model birleştirmenin arkasındaki teknikler daha iyi anlaşıldıkça ve geliştirildikçe, performanslı LLM’lerin gelişiminde köşe taşı haline gelmesi beklenmektedir. Bu yazı bu konudaki yüzeysel bir bakış açısı sunmaktadır; devam eden güncellemelerle birlikte daha birçok teknik hâlâ geliştirilmektedir. Model birleştirme, üretken AI ortamında gelişen bir alan olarak öne çıkmaktadır ve bu alanda daha fazla uygulama test edilmekte ve kanıtlanmaktadır.