Kuantum dinamikleri, kuantum mekaniği yasalarına uyan nesnelerin çevreleriyle nasıl etkileşimde bulunduğunu tanımlar. Bu etkileşimler, maddenin nasıl davrandığına dair tahminlerde bulunmamızı sağlar. Doğru kuantum dinamiği simülasyonları, yeni malzemelerin, güneş hücrelerinin, batterilerin, sensörlerin ve daha birçok ileri teknoloji ürününün geliştirilmesine yardımcı olur. Ayrıca, kuantum bilgisayarları tasarlama sürecinde de kritik bir araçtır; bu süreçte yeni tipte qubitler tasarlamak, kapı güvenilirliklerini artırmak ve cihaz kalibrasyonu yapmak gibi hedefler bulunur.
Ancak, kuantum sistemlerini simüle etmek son derece zordur. Bir dinamik simülasyonun standart adımları, bir kuantum durumunu hazırlamak, zaman içerisinde evrimini gerçekleştirmek ve sonra sistemin ortalama enerjisi ya da enerji seviyeleri arasındaki geçiş olasılıkları gibi bazı özelliklerini ölçmeyi içerir. Uygulamada, bu süreç, Schrodinger Denklemi ya da Lindblad Usta Denklemi tarafından yönetilen diferansiyel denklemleri çözmeyi gerektirir. Çok parçalı kuantum sistemleri, büyüklükleri üstel şekilde artan Hilbert Alanları tarafından temsil edilir; bu durum, geleneksel simülasyon yöntemleri ile tam çözümleri elde etmeyi imkansız hale getirir.
Bunu aşmak için, akıllı yaklaşımlar ve sayısal yöntemler kullanılmaktadır. Zorluk, hesaplama verimliliğini korurken yüksek bir doğruluk derecesi sunan yaklaşık yöntemleri bulmaktır. Tensör ağları, büyük ölçekli kuantum sistemlerinin dinamiklerini hesaplamakta oldukça etkilidir; ancak, yüksek dereceli dolanıklıklarla başa çıkmakta zorlanmaktadır. Simülasyon tekniklerinin ulaşımını daha geniş bir alana yaymak ve daha ilginç ve ilgili sistemleri keşfetmek için yeni araçlara ihtiyaç vardır.
Yeni Bir Simülasyon Yöntemi: Akış Denklemleri
Berlin Free Üniversitesi’nden araştırmacılar Jens Eisert ve Steven Thomson, kuantum dinamiklerini simüle etmek için güçlü bir yeni yöntem geliştirdi. Akış Denklemleri Kullanarak Kuantum Dinamiklerini Çözmek başlıklı makaleleri, bu sistemleri simüle etmek için güçlü bir GPU hızlandırmalı yöntem sunuyor.
Jens ve Steven, kuantum sistemlerini simüle etme zorluğunu akış denklemleri yöntemi ile çözdü. Bu yöntem, tek bir kuantum durumunu almak ve onu zamanla evrimleştirmek yerine, kuantum sistemini tanımlayan Hamiltonyen matrisini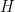 
diagonalize etmektedir. Bu, başlangıç 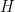üzerine çok sayıda sonsuz küçük birim dönüşüm (
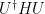, burada 
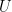bir birim matrisidir) uygulayarak gerçekleştirilir.
Tam birim dönüşümü, akış zamanı değişkeni üzerinden zamanla sıralanmış bir integral ile yapılır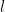 
. Zamanla sıralanmış bir integral, her adımın Hamiltonyen’in evrimiyle eş zamanlı olarak gerçekleştiğini güvence altına alır. Bu sayısal işlem, GPU’ların kullanılmasıyla verimli bir şekilde paralelleştirilebilir ve sistemin dinamiklerini simüle etmeye dair pratik bir yaklaşım sunar.
Akış Denklemlerinin Avantajları
Akış denklemlerinin en büyük avantajı, simülasyonun dolanıklılık derecesiyle sınırlı olmaması, ancak sayısal prosedürün istenen doğruluğuyla kısıtlı olmasıdır. Bu, hatanın matematiksel bir kesme olduğunu ve dolanıklılık engeli denilen kısıtlamalardan çok daha az kısıtlayıcı olduğunu gösterir. Ayrıca, daha yüksek doğruluk gerektiğinde, sistematik olarak iyileştirilip geliştirilebilir.
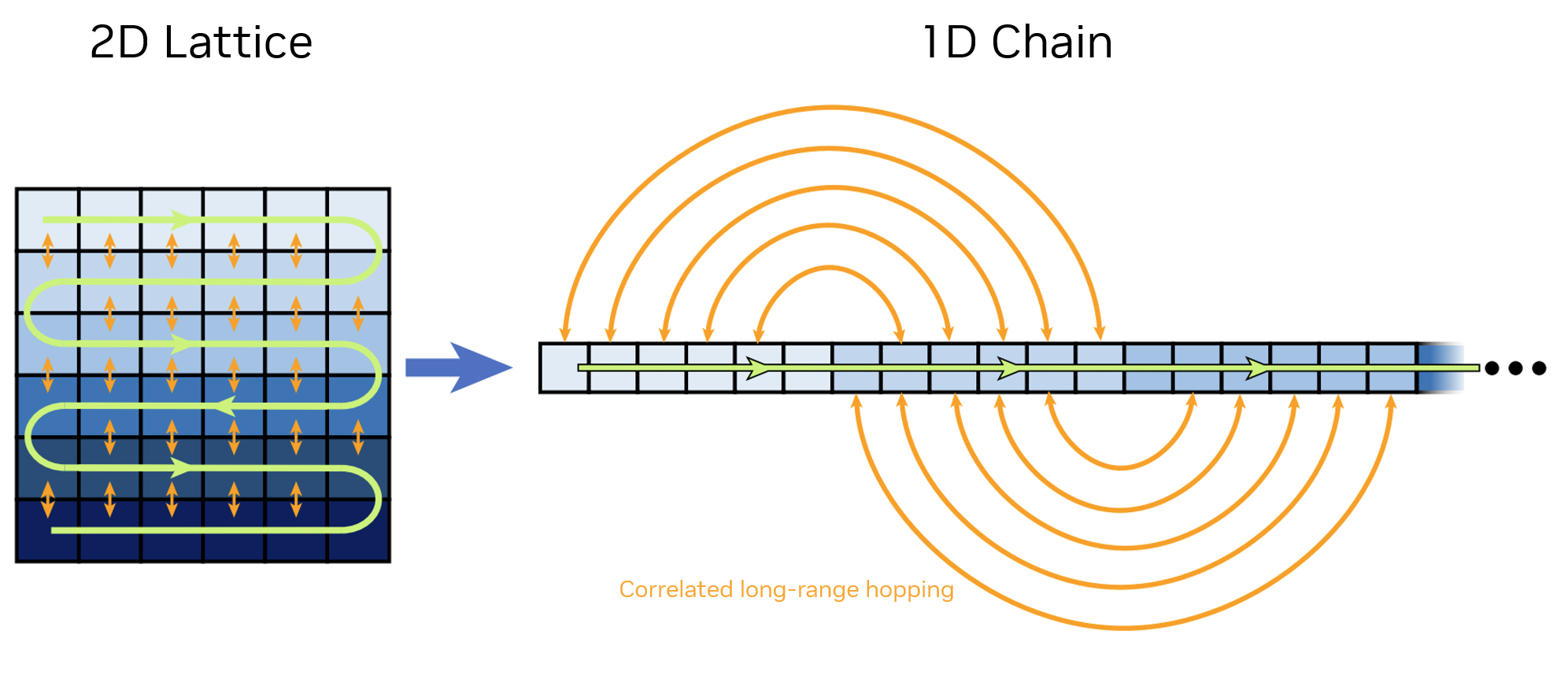
İkinci avantaj, iki ya da üç boyutlu bir sistemin kolayca “açılarak” bir boyutlu bir temsil haline getirilebilmesi ve akış denklemleri ile çözülebilmesidir. Çok boyutlu sistemleri simüle etme yeteneği, genellikle birden fazla boyutun dikkate alınmasını gerektiren gerçek dünya kuantum uygulamaları için kritik öneme sahiptir.
Yeni Bir Yaklaşım: Karıştırma Dönüşümleri
Ancak, akış denklemleri kuantum dinamiklerini simüle etmek için kesin bir çözüm sunmamaktadır. Özellikle başlangıç Hamiltonyen’inin benzer enerjiye sahip birden fazla durumu olduğunda yaklaşım zorluk yaşamaktadır; bu durum bazı ilginç vakalarda yaygındır. Bu yüzden Jens ve Steven, karıştırma dönüşümleri kullanma fikrini önerdi. Bu dönüşümler, başlangıç Hamiltonyenini “karıştırarak” diagonalizasyon işleminde sorun teşkil edebilecek olan degenerasyonları ortadan kaldırmaya yardımcı olur.
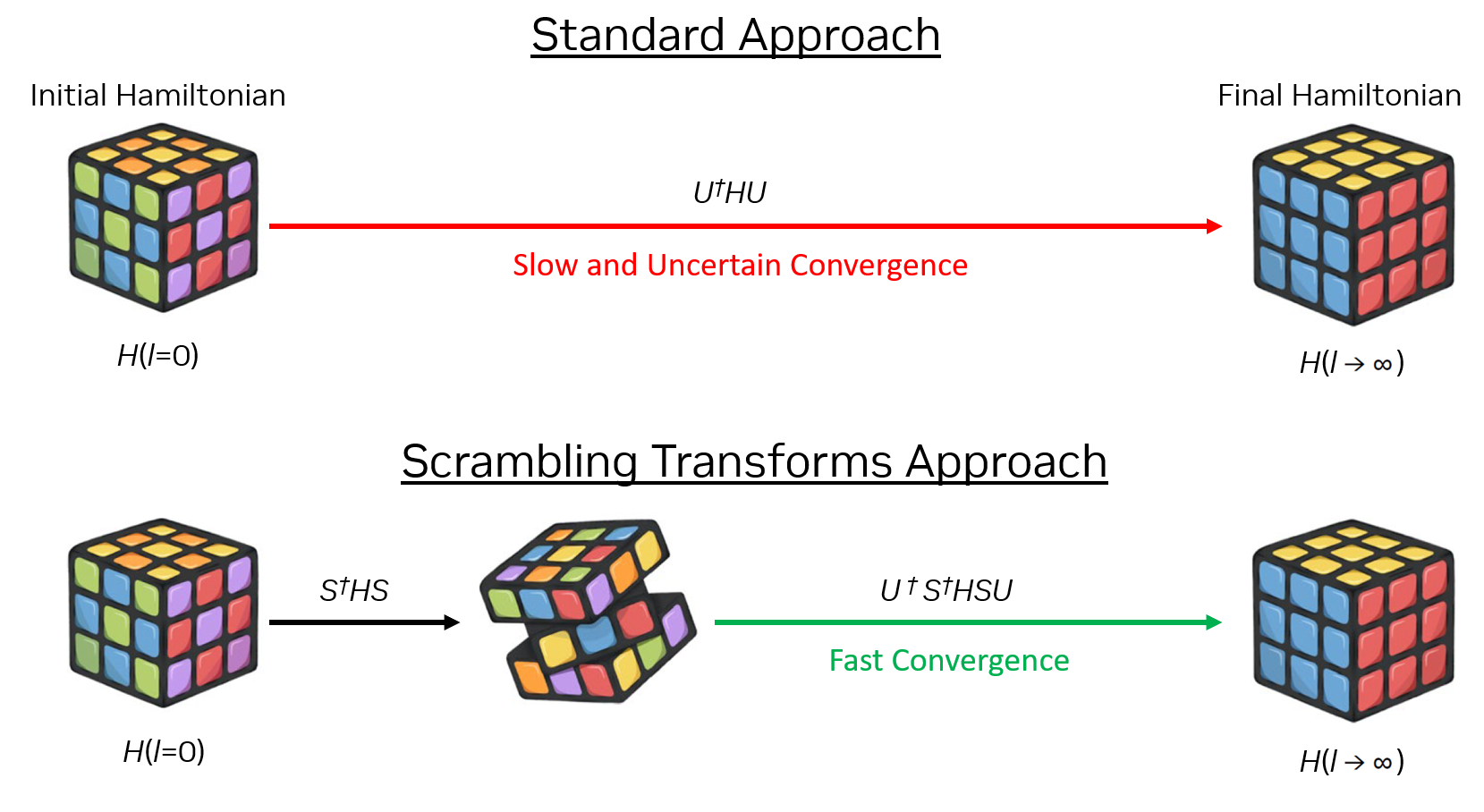
GPU Destekli Simülasyonlar ve Gelecek Perspektifi
Akış denklemleri tekniği çoğunlukla analitik çalışmalara dayanıyordu; derin hesaplamaların zorluklarından kaçınmak için kalem ve kâğıt kullanılıyordu. 2023’te Steven ve meslektaşı Marco Schirò, bu umut verici tekniği güçlü ve daha güvenilir bir sayısal yöntem haline getirme konusunda temel bir çalışma yayınladılar. Bunun detayları için Kuasiperiyodik Çok Parçalı Yerelleşmiş Sistemlerde Yerel Hareketlerin Bütünleri başlıklı makaleye göz atabilirsiniz.
Bu yöntem, çok sayıda temel matris ve tensör çarpımlarının verimli bir şekilde bölünebileceği için paralelleşmeye son derece uygundur. NVIDIA GPU’ları (örneğin Steven’in kullandığı NVIDIA RTX A5000), işlemleri on binlerce çekirdekte çalıştırarak, en iyi çok çekirdekli CPU’lara göre büyük bir hız artışı sağlar. CPU ve GPU hesaplamaları arasındaki fark, özellikle nispeten küçük sistemlerde ve modest GPU kaynaklarıyla hızlı bir şekilde büyümektedir.
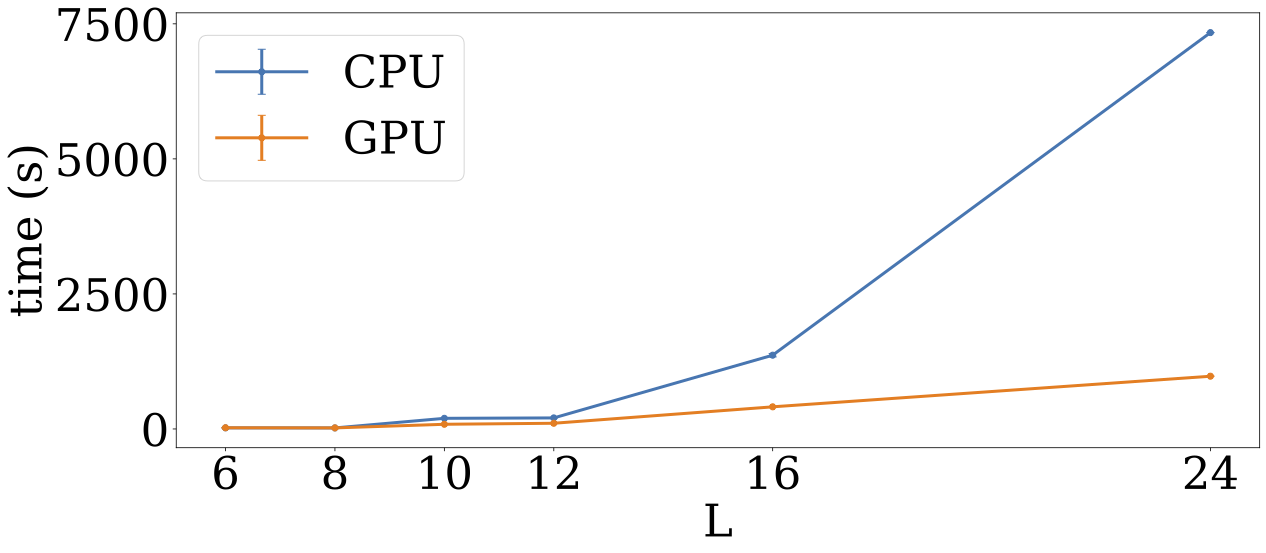
GPU’ların sağladığı hız artışı, akış denklemleri tekniğinin daha büyük ölçekli 2D sistemler için kullanılmasına olanak tanımakta; bu durum kuantum maddelerinin sayısal simülasyonları için yeni bir sınır açmaktadır.
Steven Thomson’un belirttiği gibi, “GPU’lar, bu çalışmanın başarısında kesinlikle hayati bir rol oynadı ve sayısal tekniğimizin, onların güçlü yönlerini kullanacak şekilde geliştirildi. Olmasalardı, simülasyonlarımızın çalışması on kat daha uzun sürecekti. Bu sadece beklenmeyecek kadar uzun değil, aynı zamanda simülasyonlarımıza yönelik enerji gereksinimi dolayısıyla da büyük bir çevresel maliyet doğuracaktı.”
Gelecek Vizyonu: Kuantum Dinamiklerinde Yeni Bir Boyut
Gelecek çalışmalar, daha büyük 2D ve 3D sistemler için akış denklemleri simülasyonunu ele alacak ve çoklu düğüm GPU sistemleri kullanarak kuantum dinamikleri simülasyonlarının sınırlarını daha da zorlayacaktır. Jens ve Steven’in temeli üzerine kurulu olarak, araştırmacılar daha önce hiç simüle edilmemiş daha geniş bir kuantum sistemleri yelpazesini keşfetme imkânına sahip olacaklar ve mevcut yöntemler olan tensör ağlarının güçlü ve zayıf yönlerini tamamlayacaklardır.
Araştırmanızı Hızlandırmaya Başlayın
Bu çarpıcı çalışma, bir kısmı NVIDIA Akademik Grant Programı sayesinde mümkün oldu. Bu program, araştırmacılara NVIDIA hesaplama kaynaklarına ücretsiz erişim imkânı sunarak çalışmalarını ileri taşımalarına olanak tanımaktadır. Generative AI ve büyük dil modelleri, simülasyon ve modelleme (kuantum bilgisayarlar da dahil olmak üzere), veri bilimi, grafikler ve görselleştirme ve kenar AI konularında çalışan araştırmacıların başvuruda bulunmaları teşvik edilmektedir.
NVIDIA’nın kuantum bilişim ve simülasyonla ilgili girişimleri hakkında daha fazla bilgi almak için, CUDA-Q gibi büyük ölçekli kuantum uygulamalarını geliştirmeye yönelik araçlar için NVIDIA Kuantum sayfasını ziyaret edebilirsiniz.
