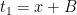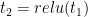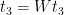nvmath-python (Beta), Python programcılarına NVIDIA’nın CUDA-X matematik kütüphanelerinden yüksek performanslı matematiksel işlemlere erişme imkanı sağlayan açık kaynaklı bir Python kütüphanesidir. Bu kütüphane, hem alt düzey bağlantılar hem de daha üst düzey Pythonic soyutlamalar sunarak programcıların işini kolaylaştırmaktadır. Aynı zamanda, PyTorch ve CuPy gibi mevcut Python paketleriyle de uyumlu çalışmaktadır.
Bu yazıda, nvmath-python’da epiloglar kullanarak matris çarpımı nasıl yapılacağını göstereceğim. Epiloglar, FFT veya matris çarpımı gibi matematiksel işlemlerle birleştirilebilen işlemlerdir. Mevcut epiloglar, en yaygın derin öğrenme hesaplamalarının çoğunu kapsamaktadır. Bu epilogların kullanımını basit bir sinir ağının ileri ve geri geçiş işlemlerini uygulayarak göstereceğim.
nvmath-python’ı kurmak için lütfen kurulum talimatlarına göz atın.
İleri geçişin RELU_BIAS epolog ile optimizasyonu
Bu bölümde, bir doğrusal katmanın ileri geçişini epiloglar kullanarak nasıl gerçekleştireceğimizi gösteriyorum. Bu katman, giriş vektörlerini bir ağırlık matrisine çarpacak, ardından sonuç matrisine bir önyargı ekleyecek ve son olarak ReLU aktivasyon fonksiyonunu uygulayacaktır.
ReLU, negatif değerleri sıfırla değiştirirken pozitif değerleri olduğu gibi bırakan yaygın kullanılan bir aktivasyon fonksiyonudur.
Matris işlemleri açısından, katmanın işlemi şu şekilde ifade edilebilir:
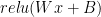
Bu eşitlikte, aşağıdaki tanımlar doğrudur:
 ,
, 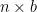 şekline sahip giriş vektörleri grubudur:
şekline sahip giriş vektörleri grubudur:
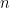 , katmanın giriş sayısını ifade eder.
, katmanın giriş sayısını ifade eder.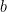 , grup boyutunu temsil eder.
, grup boyutunu temsil eder.
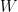 ,
, 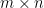 şekline sahip ağırlık matrisidir:
şekline sahip ağırlık matrisidir:
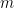 , katmanın çıkış sayısını temsil eder.
, katmanın çıkış sayısını temsil eder.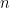 , katmanın giriş sayısını temsil eder.
, katmanın giriş sayısını temsil eder.
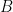 ,
, 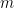 uzunluğunda bir önyargı vektörüdür; bu vektör, sonuç matrisinin her sütununa eklenir.
uzunluğunda bir önyargı vektörüdür; bu vektör, sonuç matrisinin her sütununa eklenir.
Girişlerinizi, ağırlıkları ve önyargıyı CuPy dizileri olarak tanımladığınızda:
num_inputs, num_outputs = 784, 100
batch_size = 256
weights = cupy.random.rand(num_outputs, num_inputs)
bias = cupy.random.rand(num_outputs)
x = cupy.zeros((num_inputs, batch_size))
En temel versiyonda, bu doğrusal katmanı nvmath-python kullanarak 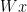 hesaplamak için uygulayabilir ve ardından önyargı ekleyerek ve ReLU fonksiyonunu manuel olarak uygulayabilirsiniz. Aşağıdaki kod örneği bu yaklaşımı göstermektedir.
hesaplamak için uygulayabilir ve ardından önyargı ekleyerek ve ReLU fonksiyonunu manuel olarak uygulayabilirsiniz. Aşağıdaki kod örneği bu yaklaşımı göstermektedir.
Bu örnekte, bir durum bilgisi olan API kullanıyorum; burada çarpma işleminin başlangıç ve planlama aşamalarını ayırabiliriz. Bu yaklaşımı kullanmam önerilir; çünkü benzer çarpımları birden fazla kez gerçekleştirecekseniz, planlamanın ilk maliyetini amorti etmenizi sağlar. Daha fazla bilgi için Matmul hakkında nvmath.linalg.advanced.Matmul dokümantasyonuna bakabilirsiniz.
mm = Matmul(weights, x)
mm.plan()
def forward():
y = mm.execute()
y += bias[:,cupy.newaxis]
y[y
Kodun performansını artırmak için RELU_BIAS epilogunu kullanarak bu üç işlemi tek bir, birleşik cuBLAS işlemi içinde gerçekleştirebilirsiniz. Bu epilog, çarpım sonucuna önyargıyı ekler ve ardından ReLU fonksiyonunu uygular.
Epilogu belirtmek için Matmul.plan metodunun epilog argümanını kullanabilirsiniz. Bazı epiloglar, RELU_BIAS gibi, ek girdiler alabilir; bunlar epilog_inputs sözlüğü içinde belirtilebilir. Epiloglar hakkında daha fazla bilgi edinmek için nvmath.linalg.advanced.Matmul dokümantasyonuna göz atabilirsiniz.
from nvmath.linalg.advanced import MatmulEpilog
mm = Matmul(weights, x)
mm.plan(epilog=MatmulEpilog.RELU_BIAS, epilog_inputs={"bias": bias})
def forward():
y = mm.execute()
return y
ReLU fonksiyonu üzerinden geriye yayılma işlemi yaparken, ReLU’ya giren hangi değerlerin pozitif olduğunu ve hangilerinin negatif olduğunu bilmeniz gerekecektir. Bu ek bilgiye ReLU maskesi denir ve RELU_AUX_BIAS epiloguyla elde edilebilir.
Bir yardımcı çıktılarla çalışan epilog kullandığınızda, Matmul.execute işlemi bir demet döndürür; bu demet gerçek sonucu ve yardımcı çıktılar sözlüğünü içerir. RELU_AUX_BIAS epilogunda, yardımcı çıktı sözlüğünün bir anahtarı olan relu_aux mevcut ReLU maskesini içerir. Bu maske bit kodlu olup, okunması zor olabilir; ancak geri geçiş sırasında bu işlemi sizin için gerçekleştiren özel epiloglar mevcuttur.
from nvmath.linalg.advanced import MatmulEpilog
mm = Matmul(weights, x)
mm.plan(epilog=MatmulEpilog.RELU_AUX_BIAS, epilog_inputs={"bias": bias})
relu_mask = None
def forward():
global relu_mask
y, aux_outputs = mm.execute()
relu_aux = aux_outputs["relu_aux"]
return y
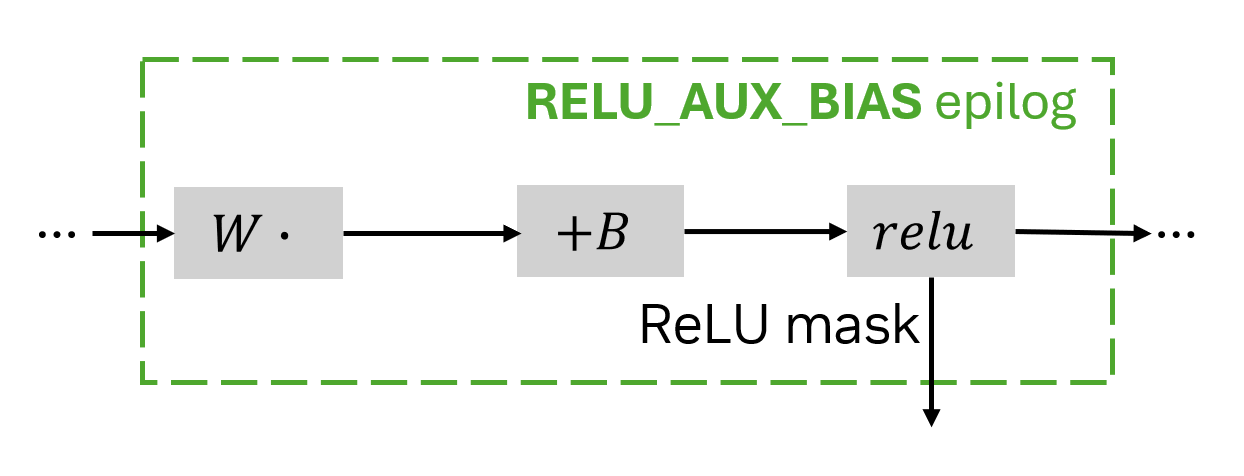
RELU_AUX_BIAS epilogunu kullanarak yapılan uygulama, naif versiyondan daha hızlıdır ve anlamlı bir performans kazancı sağlar.
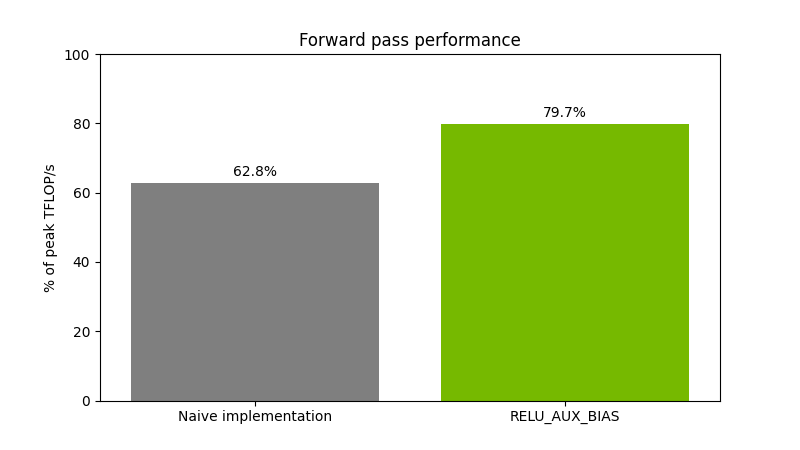
Şekil 2, (65536,16384)(16384, 8192) boyutlarındaki float16 matrislerinin çarpılması, ardından önyargı eklenmesi ve ReLU uygulanması işlemlerinin sürelerini göstermektedir. Performans, bir NVIDIA H200 GPU üzerinde ölçülmüştür.
Geri geçişin DRELU_BGRAD epilog ile optimizasyonu
Bir sinir ağının geri geçişinde, kayıp fonksiyonunun çıkışa göre gradyanı, ağı katmanlardan geri döndürülerek her bir parametre için gradyanları hesaplamak üzere yayılır.
Bir işlemin çıktısının kayıp üzerindeki etkisi bilindiğinde, bu süreçte girdilerinin ve parametrelerinin (örneğin, bir ağırlık matrisindeki değerler) kayba nasıl etki ettiği belirlenebilir. Daha fazla bilgi için Geri Yayılım makalesine başvurabilirsiniz.
Bu bölümde, arka arkaya birkaç doğrusal katman olduğunu varsayarak, önyargı ekleme, ReLU uygulama ve ağırlıklarla çarpma işlemlerinin bir dizisi üzerinden geri yayılım işlemini uyguluyorum.
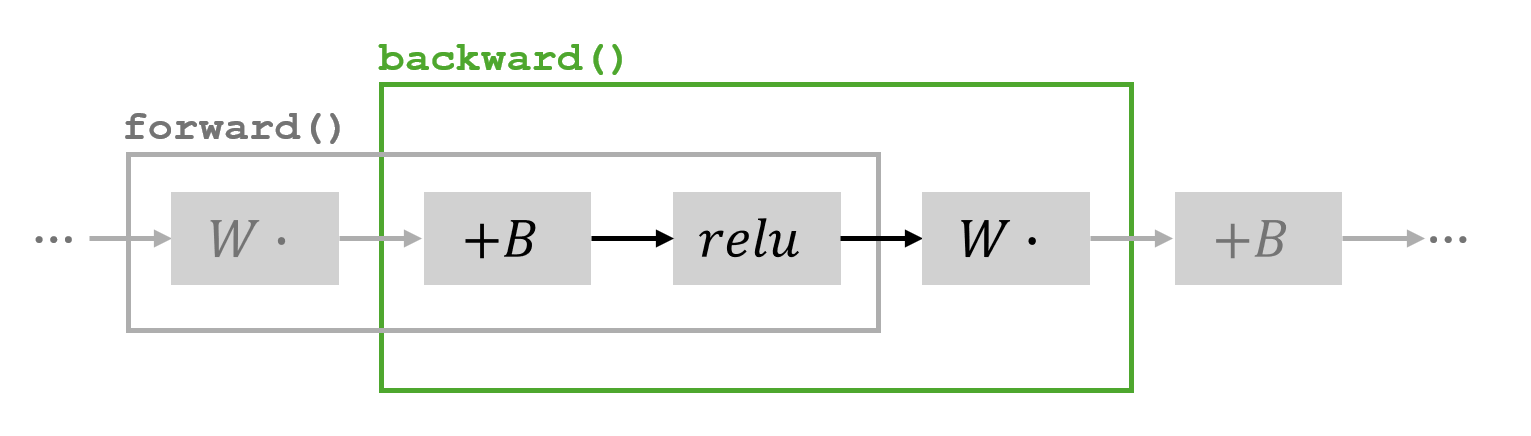
forward fonksiyonu içindeki işlemler ve backward fonksiyonu için ele alınacak kısımİleri geçişte  girişini, sırasıyla ara sonuçları
girişini, sırasıyla ara sonuçları  ,
, 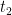 ve
ve 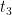 olarak gösterelim:
olarak gösterelim:
Geri yayılım sürecinde kayıp fonksiyonunun 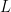 ,
, 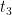 değişkenine etkisi bilindiğinde, diğer parametreler için gradyan hesaplamaları yapılabilir. Gradyanları hesaplama formüllerinin türevleri hakkında daha fazla bilgi için Otomatik Türevleme ve Sinir Ağları makalesine göz atabilirsiniz.
değişkenine etkisi bilindiğinde, diğer parametreler için gradyan hesaplamaları yapılabilir. Gradyanları hesaplama formüllerinin türevleri hakkında daha fazla bilgi için Otomatik Türevleme ve Sinir Ağları makalesine göz atabilirsiniz.
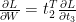
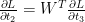
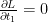 burada
burada 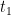 negatif,
negatif, 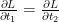 burada
burada 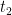 sıfırdan büyük ise geçerli.
sıfırdan büyük ise geçerli.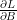
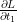 ile yine toplama yapışır.
ile yine toplama yapışır.
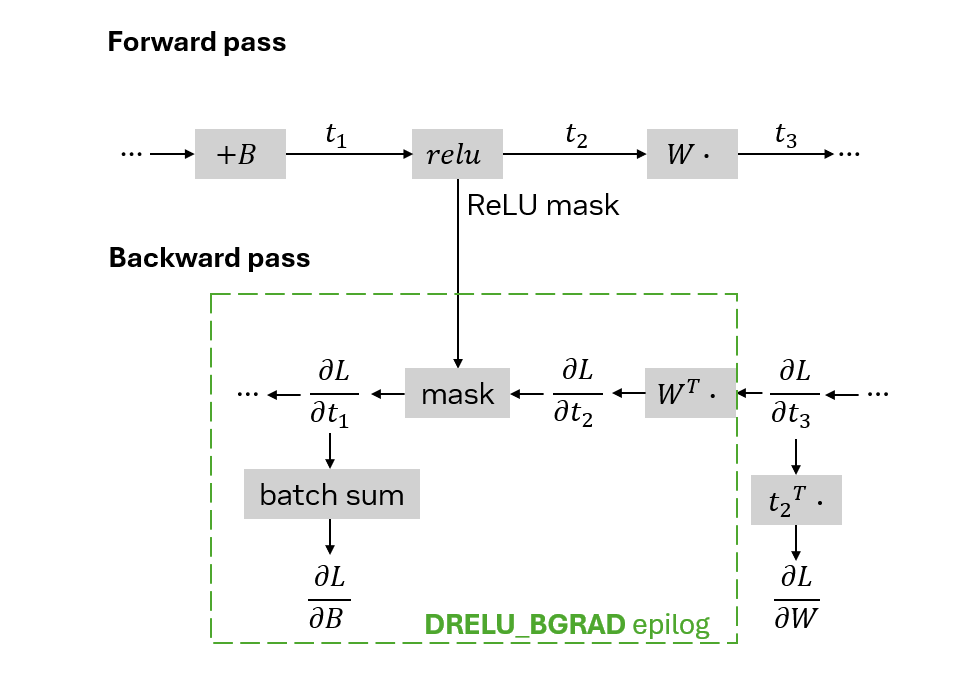
Geri geçiş esnasında 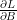 ve
ve 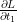 hesaplamaları naif olarak sadece Matmul kullanılarak matris çarpımı için uygulamak ve ardından maskeleme ve toplama işlemlerini manuel olarak gerçekleştirmek mümkündür:
hesaplamaları naif olarak sadece Matmul kullanılarak matris çarpımı için uygulamak ve ardından maskeleme ve toplama işlemlerini manuel olarak gerçekleştirmek mümkündür:
mm = Matmul(weights.T, grad)
mm.plan()
def backward():
grad_t1 = mm.execute()
grad_t1[mask] = 0 # varsayılan olarak `mask = (t1
Geri geçişinizi optimize etmek için DRELU_BGRAD epilogunu kullanın. Kayıtlı gradyanın 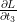 CuPy dizisinde grad olarak mevcut olduğunu varsayalım. DRELU_BGRAD epilogunun bir girdi beklediğini, bunun da RELU_AUX_BIAS epilogundan dönen maske olduğunu unutmayın. Epilog, çarpım sonucuna bu maskeyi uygular. Ayrıca sonuçla birlikte, sütun bazında toplamları sağlayan yardımcı bir çıktı döndürür; bu da
CuPy dizisinde grad olarak mevcut olduğunu varsayalım. DRELU_BGRAD epilogunun bir girdi beklediğini, bunun da RELU_AUX_BIAS epilogundan dönen maske olduğunu unutmayın. Epilog, çarpım sonucuna bu maskeyi uygular. Ayrıca sonuçla birlikte, sütun bazında toplamları sağlayan yardımcı bir çıktı döndürür; bu da 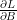 denk gelmektedir.
denk gelmektedir.
mm = Matmul(weights.T, grad)
mm.plan(epilog=MatmulEpilog.DRELU_BGRAD, epilog_inputs={"relu_aux":relu_mask})
def backward():
grad_t1, aux_outputs = mm.execute()
grad_bias = aux_outputs["drelu_bgrad"]
return grad_t1, grad_bias
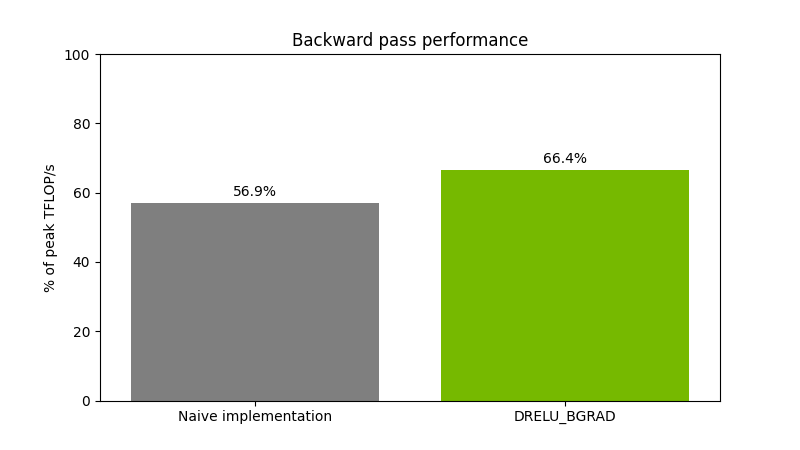
Şekil 5, (65536,16384)(16384, 8192) boyutlarındaki float16 matrislerinin çarpılması işlemi sonrası ReLU maskesi uygulaması ve önyargı gradyan hesaplaması işlemlerinin sürelerini göstermektedir. Performans, bir NVIDIA H200 GPU üzerinde ölçülmüştür.
Sonuç
nvmath-python epilogları ile yaygın derin öğrenme hesaplamalarını Python kodunuzda birleştirerek dönüşümler gerçekleştirebilir ve performansınızı büyük ölçüde artırabilirsiniz. Daha fazla bilgi için lütfen nvmath-python: NVIDIA Matematik Kütüphanelerinin Tüm Kapasitelerini Python İçinde Kullanma dokümantasyonuna bakın.
Açık kaynaklı bir kütüphane olduğumuz için, lütfen /NVIDIA/nvmath-python GitHub reposuna göz atın ve bizimle oradan iletişime geçin.